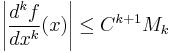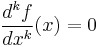Quasi-analytic function

In mathematics, a quasi-analytic class of functions is a generalization of the class of real analytic functions based upon the following fact. If f is an analytic function on an interval $[a,b] \subset \mathbb{R}$ , and at some point f and all of its derivatives are zero, then f is identically zero on all of $[a,b]$ . Quasi-analytic classes are broader classes of functions for which this statement still holds true.

Definitions

Let 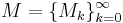$M = \{ M_k \}_{k=0}^\infty$ be a sequence of positive real numbers with 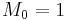$M_0 = 1$ . Then we define the class of functions $C^M([a,b])$ to be those $f \in C^\infty([a,b])$ which satisfy

$\left |\frac{d^kf}{dx^k}(x) \right | \leq C^{k%2B1} M_k$

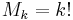for all $x\in [a,b]$ , some constant C, and all non-negative integers k. If $M_k = k!$ this is exactly the class of real analytic functions on $[a,b]$ . The class $C^M([a,b])$ is said to be quasi-analytic if whenever $f \in C^M([a,b])$ and

$\frac{d^k f}{dx^k}(x) = 0$

for some point $x \in [a,b]$ and all k, f is identically equal to zero.

A function f is called a quasi-analytic function if f is in some quasi-analytic class.

The Denjoy–Carleman theorem

The Denjoy–Carleman theorem, proved by Carleman (1926) after Denjoy (1921) gave some partial results, gives criteria on the sequence M under which $C^M([a,b])$ is a quasi-analytic class. It states that the following conditions are equivalent:

$C^M([a,b])$ is quasi-analytic
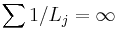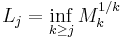
$\sum 1/L_j = \infty$ where $L_j= \inf_{k\ge j}M_k^{1/k}$
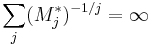$\sum_j(M_j^*)^{-1/j} = \infty$ , where M_j^* is the largest log convex sequence bounded above by M_j.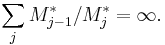
$\sum_jM_{j-1}^*/M_j^* = \infty.$

The proof that the last two conditions are equivalent to the second uses Carleman's inequality.

Example: Denjoy (1921) pointed out that if M_n is given by one of the sequences

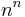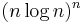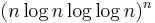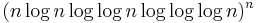$n^n$ , $(n\log n)^n$ , $(n\log n\log \log n)^n$ , $(n\log n\log \log n\log \log \log n)^n$ , …

then the corresponding class is quasi-analytic. The first sequence gives analytic functions.

References

Carleman, T. (1926), Les fonctions quasi-analytiques, Gauthier-Villars
Cohen, Paul J. (1968), "A simple proof of the Denjoy-Carleman theorem", The American Mathematical Monthly (Mathematical Association of America) 75 (1): 26–31, doi:10.2307/2315100, ISSN 0002-9890, MR 0225957, http://www.jstor.org/stable/2315100
Denjoy, A. (1921), "Sur les fonctions quasi-analytiques de variable réelle", C.R. Acad. Sci. Paris 173: 1329–1331
Hörmander, Lars (1990), The Analysis of Linear Partial Differential Operators I, Springer-Verlag, ISBN 3-540-00662
Leont'ev, A.F. (2001), "Quasi-analytic class", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=Q/q076370
Solomentsev, E.D. (2001), "Carleman theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c020430